➔ ➔
National 5 Maths: Trigonometric Graphs

Course content

  • Working with the graphs of trigonometric functions:
    • basic graphs
    • amplitude
    • vertical translation
    • multiple angle
    • phase angle

Textbook page references


Recommended revision course


A great resource to prepare for your N5 Maths exams. Get £10 discount with code 'Maths.scot'. Learn more 

Basic trig graphs

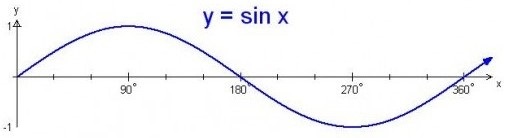
National 5 Maths - trig graphs - basic graph for sine function, y = sin x
  • Period = 360° (width of one wave)
  • Amplitude = 1 (half the height)
  • Roots: 0°, 180°, 360°
  • Maximum turning point (90,1)
  • Minimum turning point (270,–1)

 

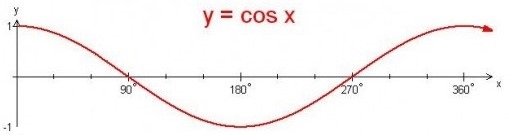
National 5 Maths - trig graphs - basic graph for cosine function, y = cos x
  • Period = 360°
  • Amplitude = 1
  • Roots: 90°, 270°
  • Maximum t.p. (0,1) and (360,1)
  • Minimum turning point (180,–1)
  • It's the sine graph moved left 90°

 

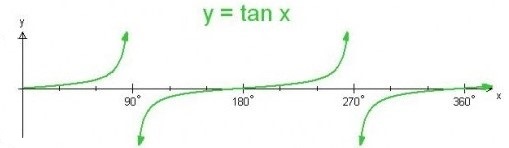
National 5 Maths - trig graphs - basic graph for tangent function, y = tan x
  • Period = 180°
  • Amplitude is undefined
  • Roots: 0°, 180°, 360°
  • No maximums or minimums
  • "Asymptotes" at \(x\) = 90° and 270°

Change of amplitude

Now we will use the sine function to look at change of amplitude and the other three transformation types that you need to understand for Nat 5 Maths.

Example:  \(y=5\small \ \normalsize sin\ x\)

  • Amplitude 5 (vertical stretch: \(\times\)5)
  • Maximum turning point (90,5)
  • Minimum turning point (270,–5)

Example:  \(y=\small \frac{1}{2}\tiny \ \normalsize\normalsize sin\ x \)

  • Amplitude \( \small \frac{1}{2}\) (vertical shrink: ÷2)
  • Maximum turning point (90,\( \small \frac{1}{2}) \)
  • Minimum turning point (270,\( –\small \frac{1}{2} \))

Example:  \(y=-sin\ x\)

  • Amplitude remains 1
  • Reflects in the \(x\)-axis (upside-down)
  • Maximum turning point (270,1)
  • Minimum turning point (90,–1)

Example:  \(y=-3\small \ \normalsize sin\ x \)

  • Amplitude 3 (vertical stretch: \(\times\)3)
  • The graph also reflects in the \(x\)-axis
  • Maximum turning point (270,3)
  • Minimum turning point (90,–3)

Vertical translation

Example:  \( y=sin\ x+2 \)

  • The basic graph moves up 2
  • Maximum turning point (90,3)
  • Minimum turning point (270,1)

Example:  \( y=sin\ x-1 \)

  • The basic graph moves down 1
  • Maximum turning point (90,0)
  • Minimum turning point (270,–2)

Vertical transformations

Now let's combine a change of amplitude and a vertical translation.

Example:  \(y=2\small \ \normalsize sin\ x+3\)

  • First, the amplitude doubles
  • Then that graph moves up 3
  • Maximum turning point (90,5)
  • Minimum turning point (270,1)

Example:  \(y=\small \frac{1}{2}\tiny \ \normalsize \normalsize sin\ x-1\)

  • First, the amplitude halves
  • Then that graph moves down 1
  • Maximum turning point (90,\( \small -\frac{1}{2} \normalsize \))
  • Minimum turning point (270,\( \small -\frac{3}{2} \normalsize \))

Example:  \(y=-2\small \ \normalsize sin\ x+5\)

  • Amplitude \( \times \)2 (double-height)
  • Reflect in the \(x\)-axis (upside-down)
  • Then move the graph up 5
  • Maximum turning point (270,7)
  • Minimum turning point (90,3)

Multiple angle

Example:  \(y=sin\ 2x\)

  • Each \(x\)-value divides by 2
  • Horizontal shrink: half-width
  • The period is 360 ÷ 2 = 180°
  • There are 2 cycles from 0° to 360°
  • Roots 0°, 90°, 180°, ...

Example:  \(y=sin\ \small \frac{1}{3}\normalsize x\)

  • Each \(x\)-value divides by \(\small \frac{1}{3}\), i.e. \(\times\)3
  • Horizontal stretch: triple-width
  • The period is 360 ÷ \(\small \frac{1}{3}\) = 1080°
  • There is \(\small \frac{1}{3}\) of a cycle from 0° to 360°
  • Roots 0°, 540°, 1080°, ...

Example:  \(y=sin\ (-4x)\)

  • Each \(x\)-value divides by –4
  • Horizontal shrink: quarter-width
  • Also a reflection in the y-axis
  • The period is 360 ÷ 4 = 90°
  • There are 4 cycles from 0° to 360°
  • Roots 0°, 45°, 90°, 135°, ...
  • The SQA has never set a question with a negative multiple angle.

Phase angle

Example:  \(y=sin\ (x-60)°\)

  • Horizontal translation: right 60°
  • Roots 60°, 240°, 420°, ...

Example:  \(y=sin\ (x+45)°\)

  • Horizontal translation: left 45°
  • Roots –45°, 135°, 315°, ...

A useful way to remember:

  • MINUS and RIGHT: 5 letters each
  • PLUS and LEFT: 4 letters each

Horizontal transformations

Now let's combine a multiple angle and a phase angle. An unexpected thing happens: the phase angle always acts before the multiple angle. PM, not MP!

Example:  \(y=sin\ (2x+60)° \)

  • First, we translate left 60°
  • Then each \(x\)-value divides by 2
  • The period is 360 ÷ 2 = 180°
  • Roots: 60°, 150°, 240°, 330°, ...

Example:  \(y=sin\ (\small \frac{1}{2}\normalsize x-30)° \)

  • First, we translate right 30°
  • Then each \(x\)-value divides by \( \frac{1}{2} \)
  • The period is 360 ÷ \( \frac{1}{2} \) = 720°
  • Roots: 60°, 420°, 780°, ...

2D transformations

Finally, we need to be able to combine horizontal and vertical transformations.

Example:  \(y=3\small \ \normalsize sin\ (x+25)° \)

  • Horizontal:
    • Translate left 25
    • No multiple angle here
    • The period remains 360°
  • Vertical:
    • Stretch: amplitude becomes 3
    • No reflection or translation
    • Max. turning point (65,3)
    • Min. turning point (245,–3)

Example:  \(y=-2\small \ \normalsize sin\ 3x - 4 \)

  • Horizontal:
    • No phase angle here
    • All \(x\)-values divide by 3
    • The period is 120°
  • Vertical:
    • Stretch: amplitude becomes 2
    • Reflect in the \(x\)-axis
    • Then translate down 4
    • Max. value: –2\(\times\)–1 – 4 = –2
    • Max. turning point (90,–2)
    • Min. value: –2\(\times\)1 – 4 = –6
    • Min. turning point (30,–6)

Example:  \(y=5\small \ \normalsize sin\ (2x-30)°+1 \)

  • Horizontal:
    • Translate right 30°
    • Then \(x\)-values divide by 2
    • The period is 180°
  • Vertical:
    • Stretch: amplitude becomes 5
    • Then translate up 1
    • Max. value: 5\(\times\)1 + 1 = 6
    • Max. turning point (60,6)
    • Min. value: 5\(\times\)–1 + 1 = –4
    • Min. turning point (150,–4)

So far, the SQA have only included two or three of the four transformation types in their questions, so that last example should have over-prepared you!

All past paper questions so far have involved a given graph, from which you need to identify either the equation or the coordinates of a turning point. Some past paper questions are explained below.

Example 1 (non-calculator)

SQA National 5 Maths 2015 P1 Q6

Part of the graph of \(y=a\,sin\,bx^\circ\) is shown in the diagram.

State the values of \(a\) and \(b\small.\)

Example 2 (non-calculator)

SQA National 5 Maths 2018 P1 Q6

Part of the graph of \(y=a\,cos\,bx^\circ\) is shown in the diagram.

State the values of \(a\) and \(b\small.\)

Recommended revision guides

How to Pass National 5 Maths 
BrightRED N5 Maths Study Guide 

Example 3 (non-calculator)

SQA National 5 Maths 2019 P1 Q13

Part of the graph of \(y=3\,cos(x+45)^\circ\) is shown in the diagram.

The graph has a minimum turning point at A. State the coordinates of A.

Example 4 (non-calculator)

SQA National 5 Maths 2021 P1 Q13

The graph of \(y=a\,cos\,x^\circ +b\small,\) \(0\leq x\leq 360\small,\) is given.

State the values of \(a\) and \(b\small.\)

N5 Maths practice papers

Non-calculator papers and solutions 
Calculator papers and solutions 

Example 5 (non-calculator)

SQA National 5 Maths 2022 P1 Q8

Part of the graph of \(y=a\,sin\,bx^\circ\) is shown in the diagram.

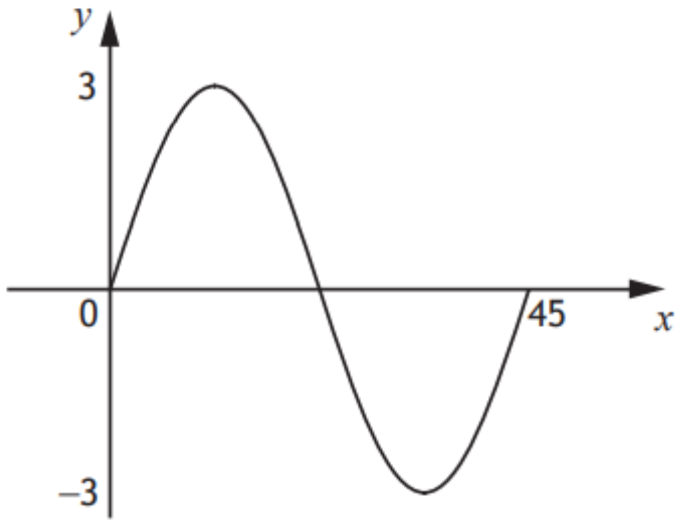
(a)  State the value of \(a\small.\)
(b)  State the value of \(b\small.\)

Example 6 (non-calculator)

SQA National 5 Maths 2023 P1 Q13

Part of the graph of \(y=cos(x+a)^\circ + b\) is shown.

(a)  State the value of \(a\small.\)
(b)  State the value of \(b\small.\)

Need a Nat 5 Maths tutor?

Just use this handy little widget and our partner Bark.com will help you find one.

Past paper questions

• All past paper questions by topic
• 2013 Specimen Paper 2 Q10(a)
• 2014 Paper 1 Q10
• 2015 Paper 1 Q6
• 2015 Paper 1 Q9 (ordering)
• 2018 Paper 1 Q6
• 2019 Paper 1 Q13
• 2021 Paper 1 Q13
• 2021 Paper 1 Q16 (with functions)
• 2022 Paper 1 Q8
• 2023 Paper 1 Q13

Other great resources

Videos - Mr Graham Maths
1. Amplitude
2. Period
3. Vertical translation
4. Phase angle
Videos - Mr Hamilton Online
1. Amplitude and period
2. Vertical shift
3. Horizontal shift
4. Summary: sin and cos
5. Trig graph exam questions
Video - YouKenMaths
Video - Tutorlene
Notes and videos - Mistercorzi
Notes and examples - Mearns Maths
PowerPoint - MathsRevision.com
Interactive graphing tool - NCTM
• Detailed notes - BBC Bitesize
• Test yourself - BBC Bitesize
Notes - Maths4Scotland
Notes - National5.com
Notes - D R Turnbull
Lesson notes - Maths 777
1. Basic, amplitude and period
2. Translations in either direction
Examples - Maths Mutt
1. Sketching trig graphs
2. Amplitude and period
Practice questions - Maths Hunter
Worksheets - Starting Points Maths
1. Maximum and minimum values
2. Horizontal transformations
3. Complete workbook
Exercises - Larkhall Academy
Pages 22-29 Ex 1-3
×

Click here to study the trig graphs notes on National5.com.

You may also want to check out their Nat 5 Maths self-study course. We think it's excellent. If you decide to enrol, just use coupon code "Maths.scot" to get £10 discount.


⇦ Nat 5 topic list  ⇧ Top of this page