
National 5 Maths
Area of a Triangle
Page sections 
- Topic content
- Textbook page numbers
- Key ideas
- Worked examples
- Past paper questions
- Worksheets
- Notes and videos
Topic content
- Calculate the area of a triangle using the trigonometric formula:
\(Area=\frac12\,ab\,sin\,C \normalsize\)
Textbook page numbers
- Zeta National 5+ Maths pp.224-225
- TeeJay Maths Book N5 pp.73-75
- Leckie National 5 Maths pp.293-298
Buy our favourite textbook
 Zeta National 5+ Maths
Zeta National 5+ Maths
Clear and comprehensive.
Progressive exercises.
Includes answers.
Buy from Zeta Press ![]()
Key ideas
- This formula works in any triangle: right-angled or non-right angled.
- This formula only needs us to know two the lengths of two sides and the angle enclosed between them.
- Unlike the other formula for the area of a triangle, \(A\!\,=\!\,\frac{1}{2}bh \), we don't need to know the vertical height.
Looking for an N5 Maths tutor?

Try our free, no-obligation tutor search tool.
Click here to find a tutor in your area. ![]()
Example 1 (calculator)

In the triangle below, BC = 9 mm, AC = 15 mm and angle C = 60°.

Calculate the area of triangle ABC.
Example 2 (non-calculator)

In the triangle below, AB = 5 cm, BC = 3 cm and sin B = \( \frac{1}{\sqrt{2}} \).

Calculate the area of triangle ABC, expressing your answer as a fully simplified surd with a rational denominator.
Example 3 (calculator)

Calculate the area of an equilateral triangle with side lengths of 5 cm.
Example 4 (calculator)

Calculate the area of a regular hexagon with side length 10 cm, giving your answer correct to 3 significant figures.
Example 5 (calculator)

A triangle of area 50 cm2 has two sides with lengths 12 cm and 10 cm. The angle between these two sides is acute. Calculate this angle.
Example 6 (calculator)

A triangle of area 50 cm2 has two sides with lengths 12 cm and 10 cm. The angle between these two sides is obtuse. Calculate this angle.
Example 7 (calculator)

SQA National 5 Maths 2015 P2 Q11
The top of a table is in the shape of a regular hexagon. The three diagonals of the hexagon which are shown as dotted lines in the diagram below each have length 40 centimetres.

Calculate the area of the top of the table.
Example 8 (non-calculator)

SQA National 5 Maths 2017 P1 Q7
In triangle DEF:
• DE = 8 centimetres
• EF = 12 centimetres
• sin E \(=\frac{2}{3}\)

Calculate the area of triangle DEF.
Example 9 (calculator)

SQA National 5 Maths 2019 P2 Q3
The diagram shows triangle PQR.

• PR = 45 centimetres
• PQ = 70 centimetres
• Angle QPR = 129°
Calculate the area of triangle PQR.
Example 10 (calculator)

SQA National 5 Maths 2023 P2 Q15
In the diagram:
• AC is perpendicular to BC
• AB = 18 centimetres
• BD = 6 centimetres
• BC = 8 centimetres.

The area of triangle ADE is 160 square centimetres.
Calculate the length of AE.
Example 11 (non-calculator)

SQA National 5 Maths 2025 P1 Q5
Triangle ABC is shown in the diagram.
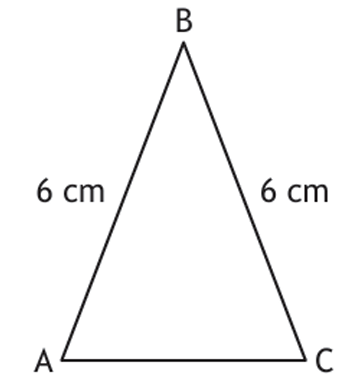
• AB = BC = 6 centimetres.
• sin B = \( \frac{2}{3}\).
Calculate the area of the triangle.
Buy N5 Maths practice papers
Zeta: Five Practice PapersCGP: N5 Maths Exam Practice
Leckie: Revision and Practice
Hodder: N5 Maths Practice Papers
Past paper questions
| • All past paper questions by topic |
|
• 2014 Paper 2 Q13 (with sector area) • 2015 Paper 2 Q11 (hexagon) • 2017 Paper 1 Q7 (non-calculator) • 2018 Paper 2 Q17 (with sector area) • 2019 Paper 2 Q3 • 2021 Paper 2 Q8 (with sector area) • 2022 Paper 2 Q6 • 2023 Paper 2 Q15 (finding a length) • 2025 Paper 1 Q5 (non-calculator) |
| Standard Grade: Credit (1986–2013) • Exam questions and answers • More exam questions and answers |
| Intermediate 2 (2000–2015) • Triangle trigonometry (with answers) |
Buy our favourite N5 textbook
 Zeta National 5+ Maths
Zeta National 5+ Maths
Clear and comprehensive.
Progressive exercises.
Includes answers.
Buy from Zeta Press ![]()
Triangle area worksheets
|
National5Maths.co.uk worksheet 1. Triangle area (with solutions) |
|
Maths Genie worksheet • Area of a triangle (Solutions) |
|
Corbettmaths worksheet • With sine/cosine rules (Answers) |
|
CJ Maths worksheet • Area of a triangle (no answers) |
| Larkhall Academy exercises • Pages 10-11 Ex 7 (no answers) |
Buy N5 Maths revision guides
How to Pass N5 MathsBrightRED: N5 Maths Study Guide
CGP: N5 Maths Revision Guide
Notes and videos
| Videos - Maths180.com |
| Video - Tynecastle HS |
| Video - Mr Graham Maths |
| Videos - YouKenMaths 1. Area of a triangle 2. Hexagon, decagon etc |
| PowerPoint - MathsRevision.com |
| Notes and videos - Mistercorzi |
| • Revision notes - BBC Bitesize • Test yourself - BBC Bitesize |
| Notes - Maths4Scotland.co.uk |
| Theory guide - National 5 Maths |
| Worked examples - Maths Mutt |
| Notes - D R Turnbull |
|
⇦ Nat 5 topic list ⇧ Top of this page
|
