National 5 Maths
Vectors

 For textbooks and tutoring, we recommend: 

Page sections

• Topic content
• Textbook page numbers
• Notation and key ideas
• Worked examples
• Past paper questions
• Worksheets
• Notes and videos

Topic content

• Adding or subtracting 2D vector pathways using directed line segments
• Adding or subtracting 2D or 3D vectors using components
• Calculating the magnitude of a 2D or 3D vector.

Textbook page numbers

• Zeta National 5+ Maths pp.234-249
• TeeJay Maths Book N5 pp.141-152
• Leckie National 5 Maths pp.312-327

Buy our favourite textbook

Zeta National 5+ Maths
Clear and comprehensive.
Progressive exercises.
Includes answers.
Buy from Zeta Press 

Notation

• \( \small \overrightarrow{\textsf{AB}} \normalsize\) represents the vector from point A to point B.
• Lower case letters are also used to represent vectors.
  • In handwriting, they are underlined, like this: \( \underline u \)
  • In print, they are in bold, like this: \( \boldsymbol u \)

Key ideas

• For any three points A, B and C,  \( \small \overrightarrow{\textsf{AC}} = \overrightarrow{\textsf{AB}} + \overrightarrow{\textsf{BC}} \normalsize \).
• Think of this as going from A to B and then continuing from B to C. In other words: from A to C via B.
• It's the same resultant journey whether we go via B or not. We start at A and end at C, so the vectors are equal. Vectors only care about the end-points, not the pathway.

Looking for an N5 Maths tutor?

Try our free, no-obligation tutor search tool.
Click here to find a tutor in your area. 

Example 1 (non-calculator)

In the diagram below, \( \boldsymbol u \), \( \boldsymbol v \) and \( \boldsymbol w \) represent \( \small \overrightarrow{\textsf{AB}} \normalsize\),  \( \small \overrightarrow{\textsf{BC}} \normalsize\) and \( \small \overrightarrow{\textsf{AC}} \normalsize\) respectively.

Express \( \boldsymbol v \) in terms of \( \boldsymbol u \) and \( \boldsymbol w \).

Show solution

Example 2 (non-calculator)

PQRS is a trapezium with \( \small \overrightarrow{\textsf{RQ}} \normalsize = 2\tiny\ \small \overrightarrow{\textsf{SP}} \normalsize \).

\( \small \overrightarrow{\textsf{PQ}} \normalsize \) and \( \small \overrightarrow{\textsf{RQ}} \normalsize \) represent vectors \( \boldsymbol u \) and \( \boldsymbol v \) respectively.

(a)  Express \( \small \overrightarrow{\textsf{RP}} \normalsize \) in terms of \( \boldsymbol u \) and \( \boldsymbol v \).
(b)  Express \( \small \overrightarrow{\textsf{RS}} \normalsize \) in terms of \( \boldsymbol u \) and \( \boldsymbol v \). Give your answer in its simplest form.

Show solution

Example 3 (non-calculator)

Given \( \boldsymbol u = \left( \begin{matrix} -4 \\ \phantom{-}5 \end{matrix} \right) \) and  \( \boldsymbol v = \left( \begin{matrix} \phantom{-}3 \\ -1 \end{matrix} \right) \), find:
  (a)\( \:\:\ \boldsymbol u + \boldsymbol v \LARGE \phantom{G} \normalsize \)
  (b)\( \:\:\ \boldsymbol u - \boldsymbol v \LARGE \phantom{G} \normalsize \)
  (c)\( \:\:\ 2\boldsymbol u - 3\boldsymbol v \LARGE \phantom{G} \normalsize \)
  (d)\( \:\:\ \frac{1}{2} \boldsymbol u + \boldsymbol v \LARGE \phantom{G} \normalsize \)

Show solution

Example 4 (non-calculator)

Given \( \boldsymbol p = \left( \begin{matrix} \phantom{-}3 \\ -2 \\ \phantom{-}1 \end{matrix} \right) \) and  \( \boldsymbol q = \left( \begin{matrix} \phantom{-}5 \\ \phantom{-}0 \\ -3 \end{matrix} \right) \), find:
  (a)\( \:\:\ 2\boldsymbol p - \boldsymbol q \LARGE \phantom{G} \normalsize \)
  (b)\( \:\:\ \frac{1}{2}\left(\boldsymbol p - \boldsymbol q \right) \LARGE \phantom{G} \normalsize \)

Show solution

Example 5 (calculator)

Find \( \vert \boldsymbol v \vert \), the magnitude of vector \( \boldsymbol v = \left( \begin{matrix} \phantom{-}45 \\ -28 \end{matrix} \right) \).

Show solution

Example 6 (calculator)

Find \( \vert \boldsymbol r \vert \), the magnitude of vector \( \boldsymbol r = \left( \begin{matrix} \phantom{-}8 \\ -19 \\ -4 \end{matrix} \right) \).

Show solution

Example 7 (non-calculator)

Find \( \vert \boldsymbol a - \boldsymbol b \vert \), where \( \boldsymbol a = \left( \begin{matrix} \phantom{.}5\phantom{.} \\ \phantom{.}6\phantom{.} \\ \end{matrix} \right) \) and \( \boldsymbol b = \left( \begin{matrix} \phantom{.}9\phantom{.} \\ \phantom{.}4\phantom{.} \\ \end{matrix} \right) \). Express your answer as a surd in its simplest form.

Show solution

Example 8 (non-calculator)

The diagram shows a rectangular-based pyramid, relative to the coordinate axes.

B is the point (8,6,0).

The apex D is directly above the centre of the base.

The height of the pyramid is 7 units.

(a) Express \( \small \overrightarrow{\textsf{AC}} \normalsize\) in component form.
(b) Express \( \small \overrightarrow{\textsf{AD}} \normalsize\) in component form.
(c) Determine the exact value of \( \vert \small \overrightarrow{\textsf{AD}} \normalsize \vert\small.\)

Show solution

Example 9 (calculator)

SQA National 5 Maths 2016 P2 Q3

The diagram below shows parallelogram ABCD.

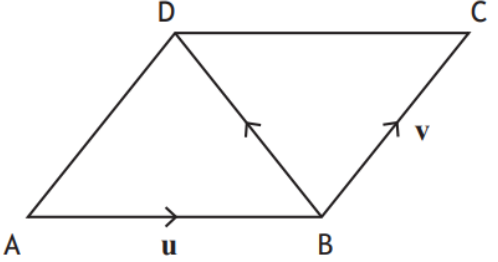
\(\small \overrightarrow{\textsf{AB}}\) represents vector \(\boldsymbol u\) and \(\small \overrightarrow{\textsf{BC}}\) represents vector \(\boldsymbol v\small.\)
Express \(\small \overrightarrow{\textsf{BD}}\) in terms of \(\boldsymbol u\) and \(\boldsymbol v\small.\)

Show solution

Example 10 (calculator)

SQA National 5 Maths 2018 P2 Q10

In the diagram below, \(\small \overrightarrow{\textsf{AB}}\) and \(\small \overrightarrow{\textsf{EA}}\) represent the vectors \(\boldsymbol u\) and \(\boldsymbol w\) respectively.

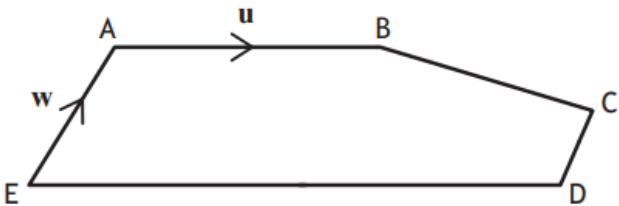
•  \(\small \overrightarrow{\textsf{ED}}=2\small\,\overrightarrow{\textsf{AB}}\)
•  \(\small \overrightarrow{\textsf{EA}}=2\small\,\overrightarrow{\textsf{DC}}\)
Express \(\small \overrightarrow{\textsf{BC}}\) in terms of \(\boldsymbol u\) and \(\boldsymbol w\small.\)
Give your answer in its simplest form.

Show solution

Example 11 (non-calculator)

SQA National 5 Maths 2019 P1 Q10

In triangle PQR, \(\small\overrightarrow{\textsf{PR}}=\left( \begin{matrix} \phantom{-}6 \\ -4 \end{matrix} \right)\) and \(\small \overrightarrow{\textsf{RQ}}=\left( \begin{matrix} -1 \\ \phantom{-}8 \end{matrix} \right)\small.\)

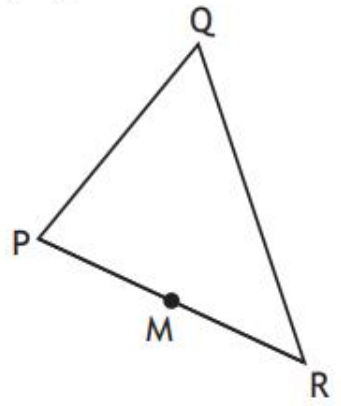
(a)  Express \(\small\overrightarrow{\textsf{PQ}}\) in component form.

M is the midpoint of PR.
(b)  Express \(\small\overrightarrow{\textsf{MQ}}\) in component form.

Show solution

Example 12 (non-calculator)

SQA National 5 Maths 2021 P2 Q5

The vectors \( \boldsymbol u \) and \( \boldsymbol v \) are shown in the diagram below.

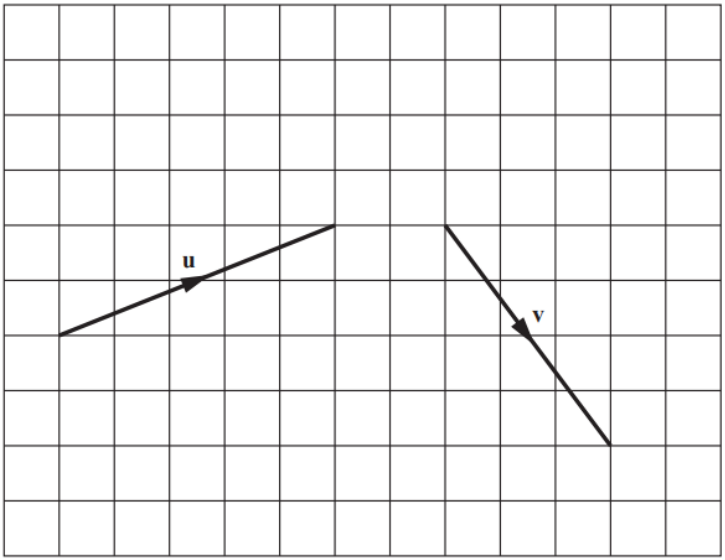
Find the resultant vector \( \boldsymbol u - \boldsymbol v\small.\)
Express your answer in component form.

Show solution

Example 13 (calculator)

SQA National 5 Maths 2021 P2 Q17

The triangle ABC is shown below

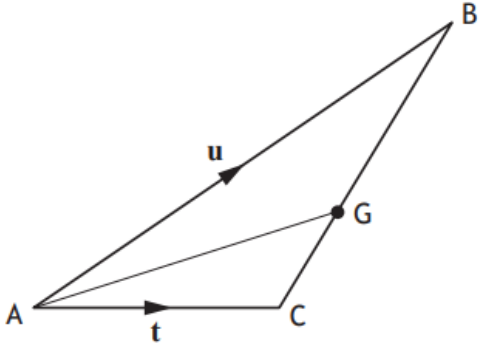
\(\small\overrightarrow{\textsf{AB}}\normalsize =\boldsymbol u\) and \(\small\overrightarrow{\textsf{AC}}\normalsize=\boldsymbol t\small.\)
G is the point such that CG = \(\large\frac{1}{3}\)CB.
Express \(\small\overrightarrow{\textsf{AG}}\) in terms of \(\boldsymbol u\) and \(\boldsymbol t\small.\)
Give your answer in simplest form.

Show solution

Example 14 (non-calculator)

SQA National 5 Maths 2024 P1 Q4

Given \( \boldsymbol a = \left( \begin{matrix} \phantom{-}3 \\ \phantom{-}4 \\ -1 \end{matrix} \right) \) and  \( \boldsymbol b = \left( \begin{matrix} 5 \\ 3 \\ 2 \end{matrix} \right)\small, \) find the resultant vector \(3\boldsymbol a + \boldsymbol b\small.\) Express your answer in component form.

Show solution

Buy N5 Maths practice papers

Zeta: Five Practice Papers   TOP CHOICE
CGP: N5 Maths Exam Practice 
Leckie: Revision and Practice 
Hodder: N5 Maths Practice Papers 

Past paper questions

• All past paper questions by topic

Vector pathways: • 2016 Paper 2 Q3 • 2017 Specimen Paper 1 Q11 • 2017 Paper 2 Q8 • 2018 Paper 2 Q10 • 2021 Paper 2 Q17 • 2024 Paper 2 Q14 • 2025 Paper 2 Q15

Vector components: • 2014 Paper 1 Q4 • 2015 Paper 2 Q5 • 2016 Paper 1 Q1 • 2018 Paper 1 Q4 • 2019 Paper 1 Q10 • 2021 Paper 2 Q5 • 2024 Paper 1 Q4 • 2025 Paper 1 Q13

Magnitude: • 2015 Paper 2 Q4 • 2017 Specimen Paper 1 Q3 • 2017 Paper 2 Q1 • 2018 Paper 2 Q3 • 2019 Paper 2 Q2 • 2021 Paper 1 Q1

Buy our favourite N5 textbook

Zeta National 5+ Maths
Clear and comprehensive.
Progressive exercises.
Includes answers.
Buy from Zeta Press 

Vectors worksheets

Maths.scot worksheet • Vectors (Answers)

Essential Skills worksheet • Vectors (Answers)

Corbettmaths worksheets 1. Column vectors (Answers) 2. Vector pathways (no answers)

National5Maths.co.uk worksheets 1. Adding vectors (with answers) 2. Column vectors (with answers) 3. Mixed questions (no answers)

CJ Maths worksheet • Vectors (no answers)

Maths Hunter worksheet • Practice questions - Maths Hunter

Cumnock Academy worksheet • Vectors (no answers)

Larkhall Academy exercises • Pages 19-32 Ex 1-8 (no answers)

MyMathsGuy.com worksheet • Vectors (with answers)

Buy N5 Maths revision guides

How to Pass N5 Maths    TOP CHOICE
BrightRED: N5 Maths Study Guide 
CGP: N5 Maths Revision Guide 

Notes and videos

Videos - Maths180.com

Videos - Mr Graham Maths 1. Introduction to vectors 2. Alternative routes 3. Magnitude of a vector 4. Scalar multiplication 5. Vector pathways

Video - Mr Hamilton Online Resultant and magnitude

Videos - YouKenMaths 1. 2D vectors 2. Vector journeys: 1 of 4 3. Vector journeys: 2 of 4 4. Vector journeys: 3 of 4 5. Vector journeys: 4 of 4 6. Worked examples

Notes and videos - Mistercorzi 1. 2D vectors 2. 3D vectors

Theory guide - National 5 Maths

PowerPoint - MathsRevision.com

Detailed notes - BBC Bitesize 1. 2D vectors 2. Vector components 3. Magnitude of a vector

Notes - National5.com

Notes - D R Turnbull

Notes and examples - Maths Mutt

⇦ Nat 5 topic list  ⇧ Top of this page